真空热处理炉加热过程的三维数值分析

摘要：
    三维数值传热模型与智能PID温度控制子程序相结合，已有了一定的发展并且应用于计算机模拟加热过程的典型真空热处理炉的负载范围内。在负载范围内获得的瞬态温度场和热滞时间，最大温差，加热温度和加热率之间的关系进行了详细的分析。结果表明，在负载范围内的最大温差，随热滞时间而降低，随加热速率而增加。一套由定性关系指导设计的真空热处理的热时间表被提出，从而实现了一个最佳的加热过程， 这不仅可以减少相当多的加热时间，而且还有效地节约能源。模拟加热曲线在某些点上与实验符合的很好，这验证了数值模拟可以用于此项研究。

关键词：温度场;传热;数值分析;热滞时间;真空热处理

1.引言：

      就加热过程在负载下处理的最终组织和性能来说，是真空热处理工艺中最重要的一个阶段。在此加热过程中，将消耗大量的能源。因此，优化加热过程对节能和控制质量来说是十分有意义的。因为在真空炉中的加热主要受辐射传热的影响，真空炉的热容量小，负载的温度上升远低于普通热处理炉。这种现象被称做热滞后。因此，在真空加热过程中有必要考虑热滞时间。

    真空热处理以辐射加热为主，其特点是炉膛升温速度比工件升温速度快得多。一方面由于炉膛的隔热材料大多采用石墨毡和陶瓷纤维，这类材料的热容量小，保温性能好，因此，炉膛的热惯性小，升温速度快。另一方面，由于炉内气体极为稀薄，加热元件对工件的传热方式以辐射传热为主，对流传热作用极其微弱，所以，工件的升温速度很慢。故存在加热滞后时间的问题。真空热处理加热保温时间实际上是由以下两部分组成的，一是工件透烧时间（即温度均匀化时间，也就是我们所讨论的加热滞后时间；，二是组织转变的时间。任何方式的热处理加热保温时间实际上均是由这两部分构成的，只不过由于真空热处理的加热方式很特殊，所以使第一部分（即加热滞后时间）成为比较突出的问题。

影响工件在真空炉中加热滞后时间的因素有工件的材料、尺寸、形状和表面光亮度，以及加热温度与加热方式、装炉量与装炉方式等。本试验是在真空炉上进行的。      

由于工件在真空中加热的升温速率比在箱式空气炉中加热慢，比在盐浴炉中加热更慢，因此，不能沿用空气炉或盐浴炉的加热时间做为真空热处理的加热时间。只有在确定加热滞后时间后，再加上常规的组织均匀化时间，才可最终确定真空热处理的加热时间。加热滞后时间的确定办法如下所述。

（1）影响工件在真空炉中加热滞后时间的因素主要有加热温度、加热方式、装炉量及装炉方式等。
（2）真空热处理加热滞后时间的确定，可采用实测法、模拟法和经验法。
（3）只有准确、合理地确定真空热处理加热滞后时间，才能保证真空热处理的工件质量满足相关技术文件的要求，而且可以提高经济效益。

    原则上，间断式真空热处理炉的总共加热时间t，依次由三部分组成t_a，t_b ，t_c 。第一部分时间段t_a是炉内的温度从室温上升到设定的温度；下面的第二部分时间段tb即整个负载的温度均匀的达到预期的温度这段时间，即热滞时间；第三部分时间段t_c是负载最初的微观结构转变为奥氏体这段时间，通常奥氏体均匀化的时间也包括在内。总的来说，t_c完全依赖于材料的类型，而t_a与t_b则主要与加热温度，加热速度，负载的形状和大小，以及是否预热有关。因此，确定t_a与t_b的准确性成为了真空热时间表的关键。

    在过去，对真空热处理时间表已经进行了大量的实验研究，从而产生不同的以实验为依据的准则。然而，这些经典模型却与实际过程有很大的偏离。到目前为止，任然没有可供参考的准则去设计最佳热时间表。此外，上述实验方法有许多缺点，如成本高，周期长，不适用于复杂的负载或炉子。最近，计算机仿真技术模拟加热过程已在钢铁工业连续退火炉，流化床炉，回火炉，推杆式加热炉和其他加热炉上被广泛应用。Monte Carlo方法，有限差分法和有限元法已经被Mochida,Kang 和Wang分别应用于真空热处理炉传热过程的数值模拟上。但是，上述模型有其明显的局限性。同时又很少有人注意炉子的模拟加热过程。在真空热处理炉中典型的温度控制方法是pid控制器（这里pid代表比例，积分和导数）。当测量温度偏离设定温度时，将会控制加热设备加热以减少偏差。这是一个典型的信息反馈控制系统。

以真空炉和负载作为一个整体系统，建立了三维数值模型。为了模拟实际温度去控制炉子，一个智能的PID子程序在这个模型中特别发展和完善。典型负载的瞬间传热在加热过程和热滞现象之间有密切的联系。在负载上的瞬态温度梯度分布已被成功的预测，一个基于多重模拟的最优时间表也被提出。

2. 数学模型的传热

真空热处理炉的传热模型包括传导，辐射，对流。在加热过程中，真空环境没有空气，所以对流传热可以忽略。在这个模拟中所使用的传热模型可以描述如下：

能量方程：

辐射模型：

在真空炉内的辐射传热是通过离散坐标传热模型计算出的。离散坐标辐射模型解决了对有限个离散多面角，以及在全球笛卡尔坐标系（x，y，z）中每个相关矢量的方向 的辐射传热方程。它把辐射传递方程变换为一个对于在空间坐标(x,y,z)辐射强度的输送方程,并解决了许多运输方程作为他们的矢量方向。

辐射传递方程可以如下表示：

对于远离炉墙的所有方向，炉墙的辐射强度是     在整个加热过程中，炉墙冷却水的温度被认为是恒定不变的，炉子其它地方的温度和负载的温度被设定为20 ⁰C 作为初始条件。

3.模拟真空加热过程

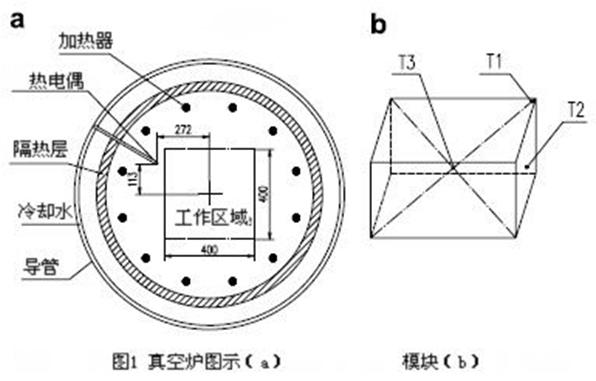
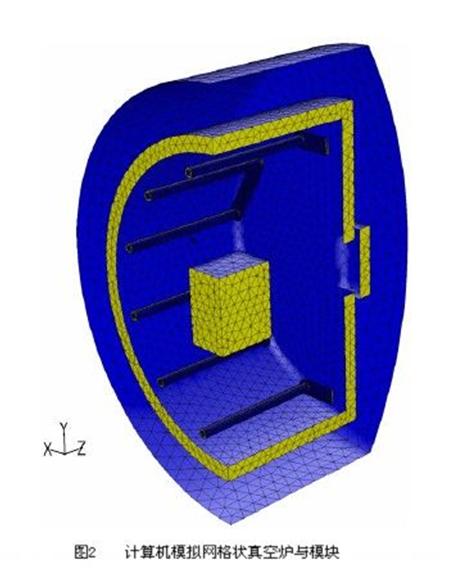
在这次工作中所用的真空热处理炉和负载分别为高压气体淬火炉模型VHQ-446HF和一片H13钢。真空炉的原理结构在图1中介绍。工作区域的面积是400×400×600（mm），最高加热温度是1320 ⁰C。炉子的加热室由带有水冷结构包围的炉膛组成，加热器由石墨管，调温热电偶，绝热炉壁组成。12个加热棒沿圆周方向均匀的分布在加热室，调温热电偶位于靠近工作区的地方。负载块的大小是230×250×370 (mm)，它位于工作区域的中心。在负载块的定位面和核心工作区域上被钻了一些孔洞（T1所指位于负载块的一角落，T2所指位于负载块一侧面的中心，T3所指位于负载块的中心）。那些孔洞直径为4mm，深度为5mm（T1和T2），T3深度为155mm，监测热电偶的具体位置如图1b所示。热处理炉的有限体积数值模型是基于商业代码Fluent 6.1产生。炉子和负载的网格形状如图2所示。炉子和负载被作为一个整体系统。通过对称，只需模拟4分之1的结构。带有调温热电偶的炉子的3维CAD模型确定以后，其数值网格模型共有41万个四面体结构

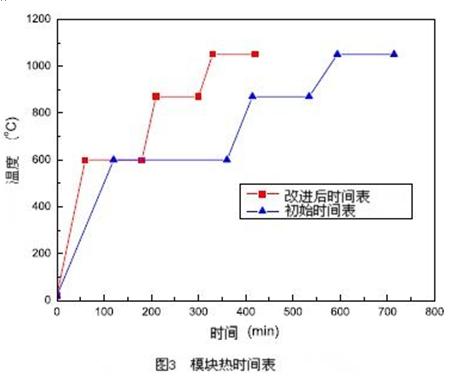
3个阶段的加热时间表和预热步骤采用以前的经验来处理（如图3所示）。在加热过程采用不同均热步骤的这段时间的预热过程，通常的设计是旨在减少在负载上温差，这样就可以减少热变形和开裂。最初的安排是，第一预热阶段的温度设定为600 ⁰C，第二阶段的温度设定为870 ⁰C，最后奥氏体化阶段的加热温度设定为1050 ⁰C。采用5 ^oC/min 的低升温速率将炉子加热到600 ^oC，在此预热温度上保温180min。然后以同样的升温速率5 ^oC/min加热到870 ^oC再保温120min。最后从870 ^oC升温到奥氏体化温度1050 ^oC期间，将升温速率减少为3 ^oC/min然后保温120min。总的加热阶段时间大概要12h，在加热过程中炉子的温度通过pid温度控制设备来控制。与此同时，在负载中特定点的加热曲线利用热电偶来测定。

 为了符合实际的加热过程，获得更准确的模拟结果，开发了从C到Fluent UDF（用户自定函数）接口的智能温度控制子程序。计算流程表以及PID控制子程序的说明见图4。改程序以用户自定初始化开始，然后从适应边界条件开始解决迭代循环。下一步得出能量方程，紧接着更新属性。PID控制子程序被称为一次迭代循环。这时由PID控制子程序读出的调温热电偶目前的温度与炉子设定的温度不同，控制系数α_pid 将被计算出，然后加热棒的源相S_h将会根据Eq来调整。（3）尽量减少错误。最后，检查收敛性和执行结束时间，决定是继续循环还是离开。

4.结果与讨论

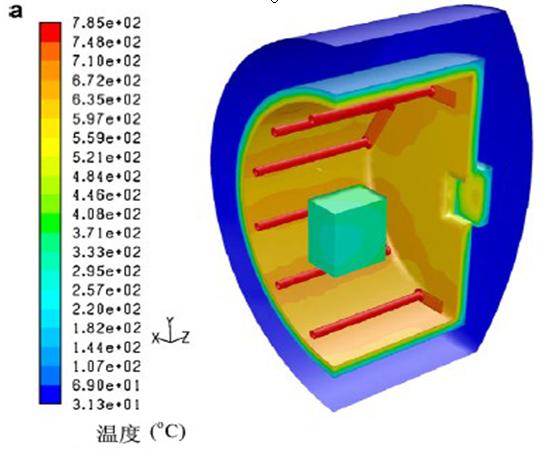
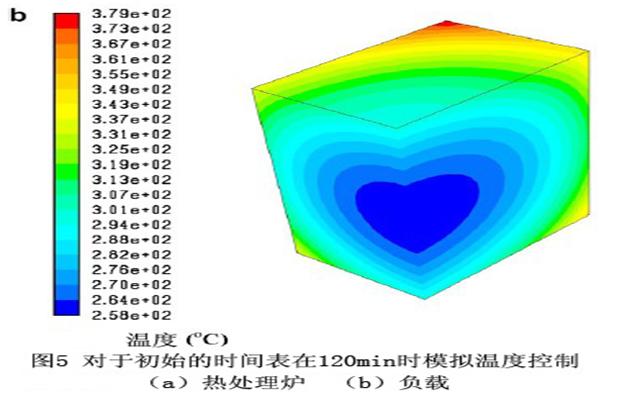
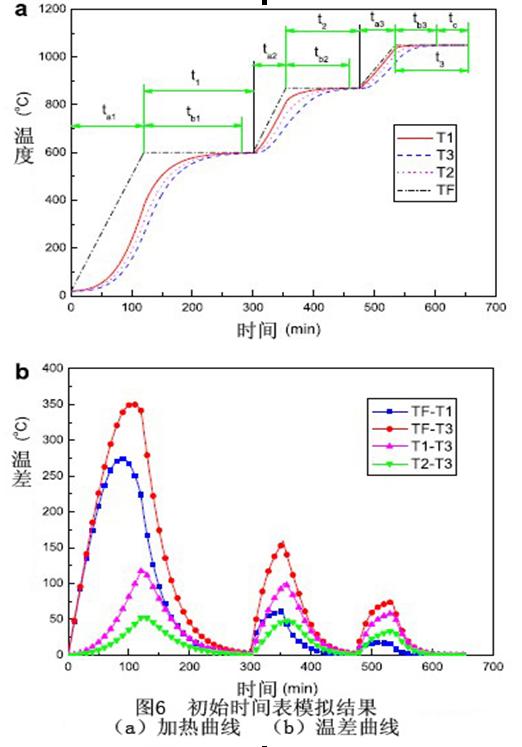
炉子和负载120min的模拟温度轮廓分别如图5a和5b所示。可以看出在炉子和负载之间存在着很大的温度梯度。同时，炉子的温度已到达开始的预热温度600 ^oC。然而，可以发现在升温速率最快的T1点的温度，也仅在379 ^oC左右。在炉子的体心（T3点）温度甚至低至258 ^oC。因此，热滞现象非常明显。图6a所示对于最初的模拟加热曲线，炉子的温度（TF）曲线得到很好的控制。因此，用户确定的PID温度控制子程序成功的模拟了真空热处理。温度的曲线和时间的曲线的不同点如图6b所示，这里在炉子和负载(TF–T3)最高温度的不同点以及负载(T1–T3)加热温度的降低，表明热滞少加热温度较高。此外，在图6a中也可以发现加热温度在600 ^oC，870 ^oC和1050 ^oC的热滞时间分别为160 min (t_b1), 100 min (t_b2) 和60 min (t_b3)。因此，热滞时间随着加热温度的降低而减少，例如：t_b1 > t_b2 >t_b3 。这可以通过在低温度范围内的低辐射传热效率来解释，这点导致负载缓慢的增加温度。原则上，设计3个加热阶段的时间表时，每个阶段所占有的时间应符合这个关系：t₁>t₂>t₃-t_c 。

这个关系也可从图6a看出t₁>t_b1和t₂>t_b2，这告诉我们第一和第二阶段的保温时间太长，超过了相关的热滞时间，导致那个负载体心的温度在第一和第二预热阶段结束前就已经达到预热温度。但是预热的目的是减少负载表面和体心的温度差，而没有到零温度差。根据美国压铸业协会（NADCA）推荐的热时间表，下一个加热阶段从表面和体心的温差不到30^oC开始。在这个意义上，第一和第二预热阶段的保温时间应相应减少以确保t₁ < t_b1 和 t₂ < t_b2。

    除此之外，对H13钢的微观结构的转变时间大概是30min，因此对于第三阶段的保温时间（t₃）应为90min（t_b3+30），同时对于起初的时间表目前的保温时间是120min。因此t₃应该被适当的减少。同样可以从图6b看出负载表面和体心的最高温差不足50 ^oC，这样，为了增加炉子的升温速率，每一步的升温时间t_a1 ，t_a2和t_a3应适当减少。

由于上述提到的非理性因素的影响，最初的热时间表需要进一步提高。产生了一个基于多重模拟的最佳时间表，它增加了第一，二和第三阶段的升温速率到10 ^oC /min, 9 ^oC C/min 和 6 ^oC C/min，分别减少每一步的保温时间到2h，1.5h和1.5h。改进后的时间表如图3所示。

改进后的模拟加热和温差曲线分别如图7a和7b所示。对比图6和图7可知在炉子和负载以及随加热速率增加的负载，这之间的最大温差，即更大的热滞影响。在第三阶段的热滞时间t_b3 可以有63min长，略长于最初的时间表。然而，在表面和体心最大温差的绝对值不到60 ^oC , ，增加幅度和最初的时间表相比大约少10 ^o, C左右。第一和第二预热阶段结束时表面（T2）和体心(T3)的温差分别不到20 ^oC和15 ^oC，按照NADCA建议的时间表的要求，因此那就存在着进一步减少预热的保温时间的可能性。在第三个加热阶段，在整个负载到达奥氏体化温度后剩下了另一个27min的组织转变。所有这一切，改进后的时间表不但符合负载的加热要求，而且相对节约了能量。总的加热时间和最初的时间表相比减少了5h。

模拟加热曲线和改进后的热时间表的实验比较如图8所示。从图可以看出，除了负载温度在800 ^oC左右这段时期外，侧表面（T2）和体心（T3）的模拟曲线与测量结果符合的很好。在此期间的偏差可能是由于相变和线性近似的一些性质。同样的，在负载一个角（T1）的模拟加热曲线也与试验结果符合的很好，只是在低温阶段时期有一个比后者相对较低的温度，这可能是由于热电偶位置的不利影响或者是温度测量系统的错误。

5结论

在这次研究中，把负载和真空炉当做一个完整的系统，建立3维瞬态传热模型，在此模型中发展PID温度控制子程序。负载块的加热过程基于此模型来模拟。得到的结论如下所示：

（1）用户定义的PID控制子程序，在模拟实际的真空炉的加热过程中，被成功的应用于控制温度，这提高了模拟的准确性。

（2）分析负载块的模拟加热过程显示：在负载以及热滞后时间的最大温差，随预热温度降低，随加热速率而增加。

（3）一些基于模拟的指导设计真空加热时间表的定性关系被提出，结果改进了加热时间表，这大大缩短了加热时间

（4）模拟结果和试验结果的对比显示：提出的数值模型在真空热处理炉中可以比较准确的预测加热过程，这种模拟为设计和改进真空时间表克以提供重要的向导。

鸣谢

   艾尔塞维尔有限公司

   这次工作得到上海技术委员会关键基础计划的大力支持。编号 06JC14036

   参考书目

[1] J. Kang, T. Huang, R. Purushothaman, W. Wang, Y. Rong,Modeling and simulation of heat transfer in loaded continuous heat treatment furnace, Transactions of Materials and Heat Treatment 25 (2004) 764–768

[2] C.P. Yan, Vacuum and Controlled Atmosphere Heat Treatment,Press of Chemical Industry, Beijing, 2006.

[3] S.Q. Zhang, Study on vacuum heat treatment thermal hysteresis time,Heat Treatment of Metals 25 (2000) 38–39.

[4] M.W. Wang, L.W. Zhang, G.D. Jiang, Numerical simulation of vacuum heat treatment thermal hysteresis time of GH4169 superalloy workpiece, Transactions of Materials and Heat Treatment 25 (2004)772–775.

[5] E. Bao, H.Y. Ren, The selection on technical parameters of vacuum heat treatment, Heat Treatment of Metals Abroad 26 (2005) 41–42.

[6] Dipl.-lng. B. Zieger, H. Schulte, Vacuum-heat treatment of hot-work steel, in: Proceedings of the Fourth International Conference on Quenching and the Control of Distortion, Chinese Heat Treatment Society, CMES, Beijing, May, 2003, pp. 401–408.

[7] F. Dong, The determination on heating time of vacuum heat treatment, Machinist Metal Forming 9 (2001) 56.

[8] J.G. Zhang, P.W. Cong, Vacuum heat treatment of hot-work die steel H13, Heat Treatment of Metals 30 (2005) 77–80.

[9] L.A. Tagliafico, M. Senarega, A simulation code for batch heat treatments, International Journal of Thermal Science 43 (2004) 509–517.

[10] A. Jaklic, F. Vode, T. Kolenko, Online simulation model of the slabreheating

process in a pusher-type furnace, Applied Thermal Engineering

27 (2007) 1105–1114.

[11] J. Harish, P. Dutta, Heat transfer analysis of pusher type reheat furnace, Ironmaking and Steelmaking 32 (2005) 151–158.

[12] D.O. Marlow, Modelling direct-fired annealing furnaces for transient operations, Applied Mathematical Modelling 20 (1996)34–40.

[13] S.H. Han, S.W. Baek, S.H. Kang, C.Y. Kim, Numerical analysis of heating characteristics of a slab in a bench scale reheating furnace,International Journal of Heat and Mass Transfer 50 (2007) 2019–2023.

[14] A. Jaklic, B. Glogovac, T. Kolenko, B. Zupancic, B. Teazk, A simulation of heat transfer during billet transport, Applied Thermal Engineering 22 (2002) 873–883.

[15] W.M. Gao, L.X. Kong, P.D. Hodgson, Numerical simulation of heat and mass transfer in fluidized bed heat treatment furnaces, Journal of Materials Processing Technology 125–126 (2002) 170–178.

[16] K.T. Januszkiewicz, Numerical model of the heating-up system with heating rods, Advances in Engineering Software 30 (1999)141–145.

[17] A. Mochida, K. Kudo, Y. Mizutani, M. Hattori, Y. Nakamura,Transient heat transfer analysis in vacuum furnaces heated by radiant tube burners, Energy Conversion and Management 38 (1997) 1169–1176.

[18] J. Kang, Y.K. Rong, W. Wang, Numerical simulation of heat transfer in loaded heat treatment furnaces, Journal De Physique IV 120 (2004)545–553.

[19] North American Die Casting Association, NADCA recommended procedures for H13 tool steel, NADCA, Rosemont Illinois,1997.